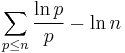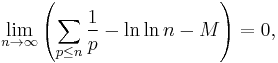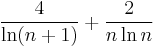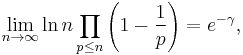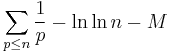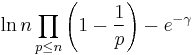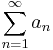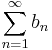Mertens' theorems

For Mertens' theorem on convergence of Cauchy products of series, see Cauchy_product#Convergence_and_Mertens.27_theorem.

In number theory, Mertens' theorems are three 1874 results related to the density of prime numbers proved by Franz Mertens (JRAM 78 (1874), 46–62). It may also refer to his theorem in analysis.

In the following, let 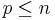p\le n mean all primes not exceeding n.

Mertens' 1st theorem:

\sum_{p \le n} \frac{\ln p}{p} - \ln n

does not exceed 2 in absolute value for every 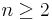n\ge 2.

Mertens' 2nd theorem:

\lim_{n\to\infty}\left(\sum_{p\le n}\frac1p -\ln\ln n-M\right) =0,

where M is the Meissel–Mertens constant. More precisely, Mertens proves (loc. cit.) that the expression under the limit does not in absolute value exceed

\frac 4{\ln(n%2B1)} %2B\frac 2{n\ln n}

for every n\ge 2.

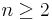Mertens' 3rd theorem:

\lim_{n\to\infty}\ln n\prod_{p\le n}\left(1-\frac1p\right)=e^{-\gamma},

where γ is the Euler–Mascheroni constant.

In a paper [1] on the growth rate of the sum-of-divisors function published in 1983, Guy Robin proved that in Mertens' 2nd theorem the difference

\sum_{p\le n}\frac1p -\ln\ln n-M

changes sign infinitely often, and that in Mertens' 3rd theorem the difference

\ln n\prod_{p\le n}\left(1-\frac1p\right)-e^{-\gamma}

changes sign infinitely often. Robin's results are analogous to Littlewood's famous theorem that the difference π(x) − li(x) changes sign infinitely often. No analog of the Skewes number (an upper bound on the first natural number x for which π(x) > li(x)) is known in the case of Mertens' 2nd and 3rd theorems.

In summability theory, Mertens' theorem states that if a real or complex infinite series

\sum_{n=1}^\infty a_n

converges to A and another

\sum_{n=1}^\infty b_n

converges absolutely to B then their Cauchy product converges to AB.

References

  1. ^ Robin, G. (1983). "Sur l’ordre maximum de la fonction somme des diviseurs". Séminaire Delange–Pisot–Poitou, Théorie des nombres (1981–1982). Progress in Mathematics 38: 233–244. 

Further reading

External links